Mapless Navigation
In this task we teach an agent to autonomously navigate to target locations using local terrain information. Below we present the rewards, neural network, and terrain environment used for this task.
Rewards
For the rover to actually learn to move, it needs some kind of indication of whether an executed action helps to accomplish the goal or not. Therefore, a set of reward functions has been implemented, evaluating if the rover moved in the right direction or if the action was beneficial in another way, e.g., to avoid a collision. For each reward function, there is a weight that defines how much influence the individual reward function has on the total reward. The weights are defined in the table below.
| Reward Function | Weight |
|---|---|
| Relative distance | $ \omega_d $ |
| Heading constraint | $\omega_h$ |
| Collision penalty | $\omega_c$ |
| Velocity constraint | $\omega_v$ |
| Oscillation constraint | $\omega_a$ |
Relative distance reward
To motivate the agent to move towards the goal, the following reward function is created: $$r_d = \frac{\omega_d}{1+d(x,y)^2},$$ where, $r_d$ is a non-negative number that will increase from a number close to zero towards 1, when the rover gets closer to the goal.
Heading constraint
This reward describes the difference between the direction the rover is heading and the goal. If the heading difference is more than 90 degrees, the agent receives a penalty to prevent it from driving away from the goal. Through empirical testing the angle is set to ±115 degrees, because the rover may sometimes need to move around objects and therefore go backwards. The mentioned penalty is defined as:
$$ r_h = \begin{cases} \vert \theta_{goal}\vert > 115^{\circ}, & -\omega_h \cdot \vert \theta_{goal} \vert \ \vert \theta_{goal}\vert \leq 115^{\circ}, & 0 \end{cases} $$
where $\theta_{goal}$ is the angle between the goal location and rover heading.
Collision penalty
If the rover collides with a rock it will receive a penalty for colliding as seen in the equation: $$r_c = -\omega_c$$
Velocity constraint
To ensure that the rover is not driving backwards to the goal, a penalty for non-positive velocities is given, implemented as follows:
$$ r_v = \begin{cases} v_{lin}(x,y) < 0 & -\omega_v \cdot \vert v_{lin} \vert\ v_{lin}(x,y) \geq 0 & 0 \end{cases} $$
where $v_{lin}$ is the linear velocity of the rover.
Oscillation constraint
To smooth the output of the neural network, a penalty is implemented to discourage sudden changes by comparing the current action to the previous action:
$$r_a = -\omega_a \sum^2_i (a_{i,t}-a_{i,t-1})^2$$
where $a_{i,t}$ is the action $i$ at time $t$.
Total reward
At each time step, the total reward is calculated as the sum of the outputs of all presented reward functions:
$$r_{total} = r_d + r_c + r_v + r_h + r_a$$
Neural Network
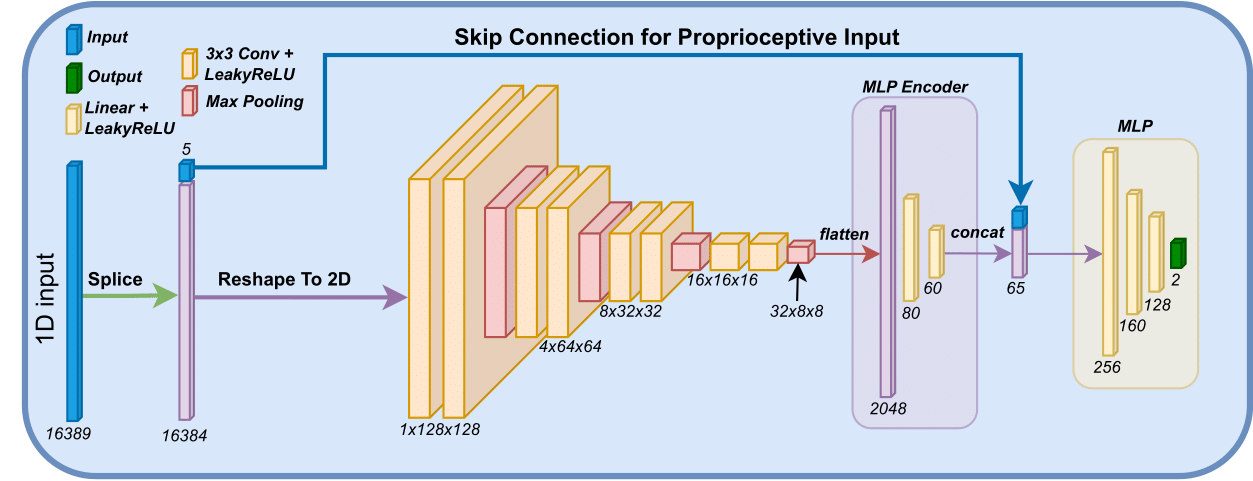
As training is performed using an on-policy method, the policy $\pi_\theta$ is modeled using a Gaussian model. The network architecture is designed to generate a latent representations of the terrain in close proximity to the rover denoted $l_t$. This is defined as
$$ l_t = e(o_t^t), $$
where $e$ are encoders for the terrain input. The encoder consist of two linear layers of size [60, 20] and utilize LeakyReLU as the activation function. A multilayer perceptron is then applied to the latent representation and the proprioceptive input as
$$ a = mlp(o_t^p, l_t), $$
where $a$ refers to the actions and $mlp$ is a multilayer perceptron with three linear layers of size [512, 256, 128] and LeakyReLU as the activation function. The network architecture is visualized below.
Environment
Below the environment used in this task in shown, it features a 200m x 200m map with obstacles.
